











Khoa Tran is an electrical engineer working at the Los Angeles Department of Water and Power and is currently pursuing his master's in electrical Power from the University of Southern California. He is fluent in both Vietnamese and English and is interested in outdoor activities and exploring new things.

.webp)
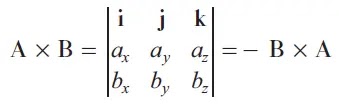
Khoa Tran is an electrical engineer working at the Los Angeles Department of Water and Power and is currently pursuing his master's in electrical Power from the University of Southern California. He is fluent in both Vietnamese and English and is interested in outdoor activities and exploring new things.

.webp)
.webp)
Khoa Tran is an electrical engineer working at the Los Angeles Department of Water and Power and is currently pursuing his master's in electrical Power from the University of Southern California. He is fluent in both Vietnamese and English and is interested in outdoor activities and exploring new things.
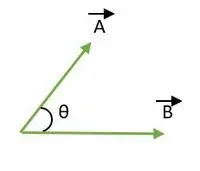
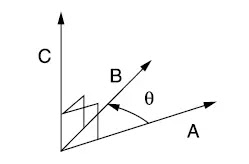
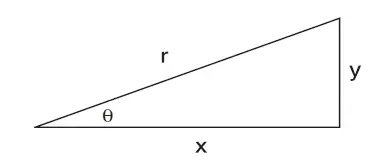
Ever wonder how auto-pilot works or how assembly robots move so quickly yet accurately? Control Systems. Not only does this apply to automation or specialized industries but also to our refrigerators, our cars, and everything where a device or system needs to have a desired output, control systems are implemented.
The FE requires examinees to understand and be able to solve questions regarding control systems. In this blog, we will go over a brief overview of what control systems are and what equations are expected for test takers to know for the exam.




|
sn |
an |
an-2 |
an-4 |
|
sn-1 |
an-1 |
an-3 |
an-5 |
|
sn-2 |
b1 |
b2 |
b3 |
|
sn-3 |
c1 |
c2 |
c3 |
|
: |
|
|
|
|
s0 |
|
|
|
|
s4 |
1 |
6 |
1 |
|
s3 |
2 |
4 |
|
|
s2 |
b1 |
b2 |
|
|
s1 |
c1 |
|
|
|
s0 |
d1 |
|
|
b1 = 2(6) - 4(1) / 2 = 4
b2 = 2(1) - 1(0) / 2 = 1
c1 = b1(4) -2(b2) / b1 = 4(4) - 2(1) /4 = 3.5
d1 = c1(b2) - b1(0) / c1 = 3.5(1)- 4(0) / 3.5 = 1
|
s4 |
1 |
6 |
1 |
|
s3 |
2 |
4 |
|
|
s2 |
4 |
1 |
|
|
s1 |
3.5 |
|
|
|
s0 |
1 |
|
|
|
s4 |
1 |
6 |
1 |
|
s3 |
2 |
4 |
|
|
s2 |
4 |
1 |
|
|
s1 |
-3.5 |
|
|
|
s0 |
1 |
|
|
Khoa Tran is an electrical engineer working at the Los Angeles Department of Water and Power and is currently pursuing his master's in electrical Power from the University of Southern California. He is fluent in both Vietnamese and English and is interested in outdoor activities and exploring new things.