
Thursday, 28 March 2024
Across State Lines: Does It Matter Where You Take Your FE Exam?

Thursday, 21 March 2024
Location Matters: The Impact of Neighborhood Context on Project Design

Adam Castelli is a licensed architect and engineer currently practicing in the Pittsburgh area. He holds a master's degree in architecture from the University of Massachusetts Amherst and a bachelor's degree in civil engineering from Villanova University.
Thursday, 14 March 2024
A Deep Dive on Digital Systems: Exploring Topics within the FE Electrical Exam Pt. 2

 Figure 1
Figure 1|
D |
Qn+1 |
|
|
0 |
0 |
Reset |
|
1 |
1 |
Set |

|
S |
R |
Qn+1 |
|
|
0 |
0 |
Qn |
No change |
|
0 |
1 |
0 |
Reset |
|
1 |
0 |
1 |
Set |
|
1 |
1 |
Indeterminate |
Indeterminate |
- The J input functions similarly to the S input of the SR flip-flop, intended to set the flip-flop to a particular state.
- The K input behaves akin to the R input of the SR flip-flop, responsible for resetting the flip-flop and changing its state (Widmer et al., 2017, 259).

|
J |
K |
Qn+1 |
|
|
0 |
0 |
Qn |
No change |
|
0 |
1 |
0 |
Reset |
|
1 |
0 |
1 |
Set |
|
1 |
1 |
Q'n |
Compliment |
- Input buffers and inverters generate both the original and complement forms of each input variable.
- A set of AND gates, where the inputs can be programmed or selected.
- A set of OR gates, where the inputs can also be programmed or selected.
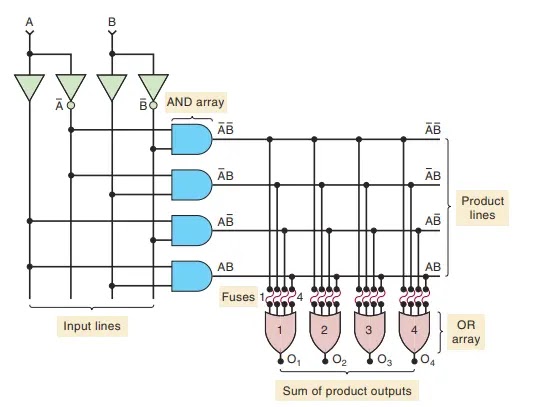
.webp)

- Obtain the function of the circuit: Understand the behavior and logic of the system to define its function.
- Determine the four main components: Identify the present state, inputs, next state, and output of the circuit. These components define the behavior and transitions within the system.
- Create a truth table: Combine the function and the four components to form a truth table. The truth table represents all possible combinations of inputs and current states, along with the corresponding outputs and next states.
- Obtain the binary result: Analyze the truth table to determine the binary representation of the system's behavior and transitions. This binary result serves as the foundation for constructing the state diagram.
|
Present state |
Inputs |
Next state |
|
|
A |
x |
y |
A |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
.webp)
Figure 7
- Static Hazards are when one input variable changes the output changes momentarily.
- Dynamic Hazards are when an output changes more than once from a single input change.
- Function Hazards are when more than one input variables change at the same time.
Khoa Tran is an electrical engineer working at the Los Angeles Department of Water and Power and is currently pursuing his master's in electrical Power from the University of Southern California. He is fluent in both Vietnamese and English and is interested in outdoor activities and exploring new things.
Thursday, 7 March 2024
A Deep Dive on Digital Systems: Exploring Topics within the FE Electrical Exam
- Number systems
- Boolean logic
- Logic gates and circuits
- Logic minimization (e.g., Sum of Product (SOP), Product of Sum (POS), Karnaugh maps)
- Flip-flops and counters
- Programmable logic devices and gate arrays
- State machine design
- Timing (e.g., diagrams, asynchronous inputs, race conditions, and other hazards)

- Decimal System
The decimal system consists of a set of 10 symbols or numerals, namely 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. By utilizing these symbols as the digits of a number, we can represent any quantity within the decimal system (Widmer et al., 2017, 19). - Binary System
In the binary system, we only have 0 and 1, and each binary digit has its own value expressed as a power of 2 (Widmer et al., 2017, 21). The concept is depicted in Figure 1, where positions to the left of the binary point, analogous to the decimal point, represent positive powers of 2, while positions to the right represent negative powers of 2. Figure 1
Figure 1 - Hexadecimal System
Hexadecimal is a numbering system represented in base 16, utilizing both numbers "0-9" and the alphabet "A-F" for double digit values "10-15". - Octal System
This numerical system is a base-8 system, using digits "0-7"
|
Logic
0 |
Logic 1 |
|
False |
True |
|
Off |
On |
|
Low |
High |
|
No |
Yes |
|
Open switch |
Closed switch |

|
A |
x |
|
0 |
1 |
|
1 |
0 |

x = A . B
The truth table is depicted below.
|
A |
B |
x = A . B |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |

x = A + B
The truth table is depicted below.
|
A |
B |
x = A + B |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Logic Minimization
SOP consists of two
or more AND terms that are ORed together. SOP can also be referred to as
Minterm. The function used to denote the sum of minterms is expressed below
(Widmer et al., 2017, 138).
The SOP is selected by f (x ,y ,z) = 1
2. Product-of-SumsPOS consists of two
or more OR terms that are ANDed together. POS can also be referred to as
Maxterm. The function used to denote the product of maxterms is expressed below
(Widmer et al., 2017, 139).
The POS is selected by F (x ,y ,z) = 0
Given the truth table below, the expression of the SOP-Minterms and POS-Maxterms for the three binary variables can be obtained.
|
A |
B |
C |
Minterms |
Maxterms |
||
|
Term |
Designation |
Term |
Designation |
|||
|
0 |
0 |
0 |
A'B'C' |
m0 |
A+B+C |
M0 |
|
0 |
0 |
1 |
A'B'C |
m1 |
A+B+C' |
M1 |
|
0 |
1 |
0 |
A'BC' |
m2 |
A+B'+C' |
M2 |
|
0 |
1 |
1 |
A'BC |
m3 |
A+B'+C' |
M3 |
|
1 |
0 |
0 |
AB'C' |
m4 |
A'+B+C |
M4 |
|
1 |
0 |
1 |
AB'C |
m5 |
A'+B+C' |
M5 |
|
1 |
1 |
0 |
ABC' |
m6 |
A'+B'+C |
M6 |
|
1 |
1 |
1 |
ABC |
m7 |
A'+B'+C |
M7 |
Example: Find the expression for the function f as (a) sum of minterms and (b) product of maxterms using the following truth table.
|
A |
B |
C | f |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |


|
A |
B |
C |
f |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |



Khoa Tran is an electrical engineer working at the Los Angeles Department of Water and Power and is currently pursuing his master's in electrical Power from the University of Southern California. He is fluent in both Vietnamese and English and is interested in outdoor activities and exploring new things.